新視Q事例研究
紹介
ここに示すケーススタディには、自由落下光球軌跡の科学的発見とシュレーディンガー猫の思考実験のシミュレーション、M 1予測コンテストのデータセット、ダウジョーンズ指数の株式取引が含まれている。新視Qは、現在表示されているデータセットを含むがこれらに限定されないさまざまなデータセットで実行できるため、このページは定期的に更新されます。
1. 科学的発見
ここでは2つの科学的発見のケーススタディを紹介した。光球の自由落下、シュレーディンガーの猫思考実験をシミュレーションする。
フリーフォール光球の事例研究は古典的で確定的な予測データセットを説明した：フリーフォール光球の軌跡は確定的であり、初期 関数を使用すると、過去を正確に再構築し、将来の軌跡を描画するための条件を得ることができます。ここで注意すべき点は、光球が 完全に固体の物体ではありません。自由落下の過程で光が 空気抵抗と重力加速度に対する球の順応性が異なる。そのため、光球の自由落下体は微積分を純粋に用いて計算することができず、これによりユニークな 予測ケーススタディ。
シュレーディンガーの猫思考実験では、猫が「同時に死ぬことと生きること」であることはよく知られているが、普通のジョーにとって、箱の中の猫が死ぬことは生きることではない。 しかし、科学者の観察者にとって、彼らの本能は箱を開ける前に、中の猫が死ぬか生きるかを「予測」するための仮説と理論を立てることだ。これはまさに私たちが利用できるもので、 シミュレーションされたシュレーディンガー猫の思考実験を使用することで、シュレーディンガーの原始的な記述（ガイガーカウンタ、放射性物質、シアン酸）に基づいて25箱の猫を生成し、 観察者や科学者は前19箱を開けて、中の猫が生きているか死んでいるかを見ることができ、それから前19箱の猫の歴史データを研究することで、「そして彼らは残り6箱の猫の状態を予測することができる」ことで、 この実験を時系列予測シーンに変えることができる。
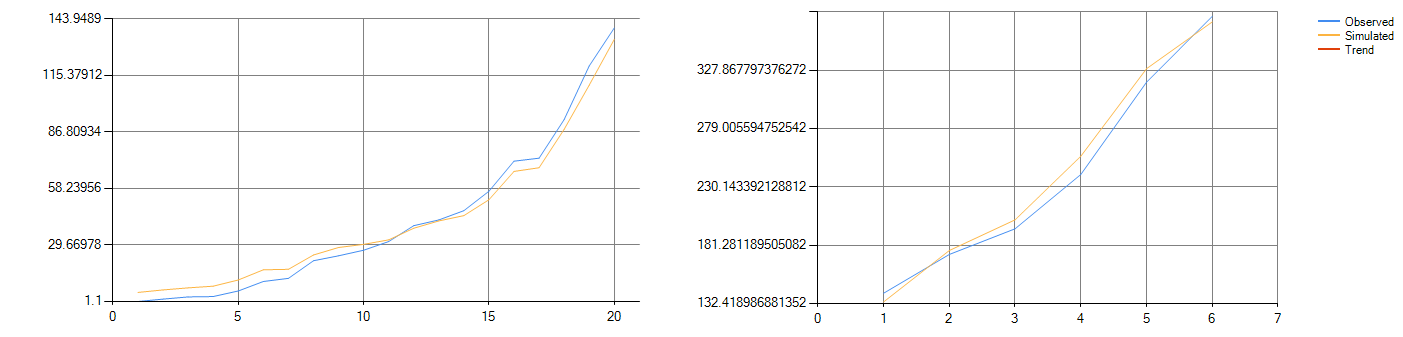図1-1：自由落下光球フィッティング（左）と予測（右）図
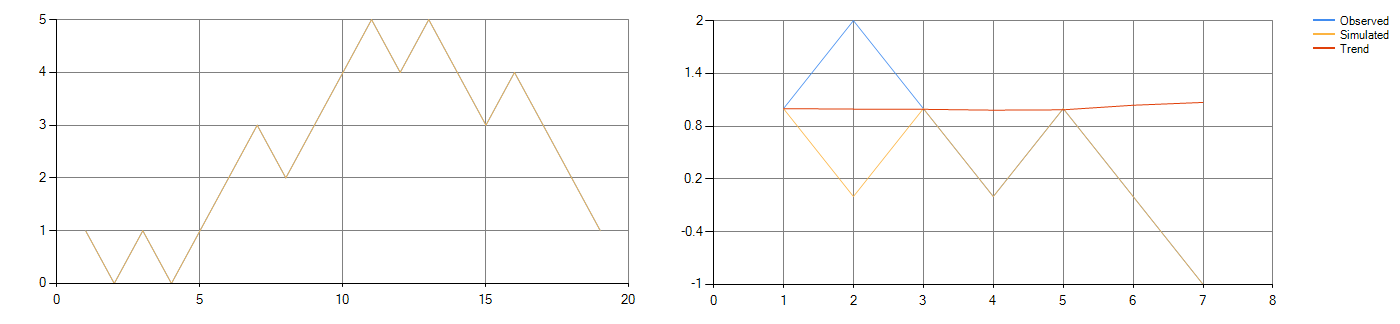図1-2：シュレーディンガー猫の思考実験フィッティングのシミュレーション（左）と予測（右）図
図1−1の左側の図形は自由落下光球のフィッティング図であり、図1−2の右側の図形は自由落下光球の予測軌跡とその「実際」軌跡の検証予測図である 未来の軌跡。図1−2の左側の図はシュレーディンガー猫の思考実験をシミュレーションしたフィッティング図であり、図1−2の右側の図は以下の6つのブロックの検証予測図である 猫の予測状態。
| ラベル | 距離の計算 | 元の距離 |
|---|---|---|
| 21 | 133.756 | 141.0 |
| 22 | 176.798 | 173.5 |
| 23 | 202.488 | 195.0 |
| 24 | 255.784 | 240.5 |
| 25 | 329.132 | 317.8 |
| 26 | 368.132 | 373.0 |
表1-1：フリーフォール光球の予測データ値の検証
| ラベル | 猫の状態を予測する | 猫の状態を観察する |
|---|---|---|
| 20 | 1 | 0 |
| 21 | 1 | 1 |
| 22 | 1 | 1 |
| 23 | 0 | 0 |
| 24 | 1 | 1 |
| 25 | 1 | 1 |
表1-2：シュレーディンガー猫の思考実験をシミュレーションする動作シーケンス
表1−1はフリーフォール光球の検証データであり、精度は96%であった。 表1−2は、「推測」ボックス20−25における猫の状態のために生成された最終的な動作シーケンスであり、0は猫が生きていることを示し、1は猫が死んでいることを示し、予測確率は83%である。
詳細については、こちらの論文をご覧ください AIアシスタント科学者：量子のような進化アルゴリズムを用いた科学的発見の支援。
2. M1予測レース
ここでは、第1回Mコンテストの年間データセットT153のケーススタディを示します。
このデータセットの独自性を考慮すると、古典的な予測と量子的な予測を実行することができ、新視Qの2元予測能力を十分に際立たせることができます。 本質的には、古典的予測の場合、新視Qは関数を生成して過去の軌跡をフィットさせ、将来の軌跡を予測することができます。量子予測については、 新視Qは、論理ツリーを使用して過去にフィットし、確率予測を生成します。
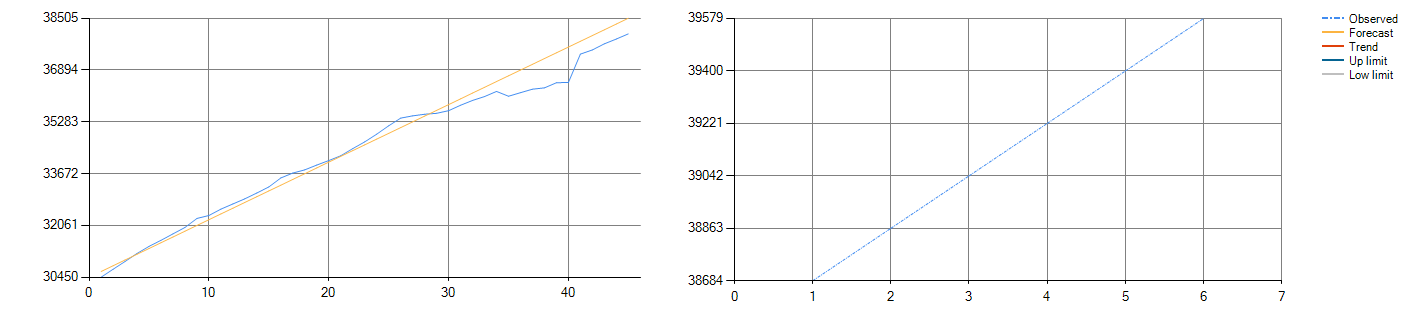図2−1：T 153古典適合（左）と予測（右）データ
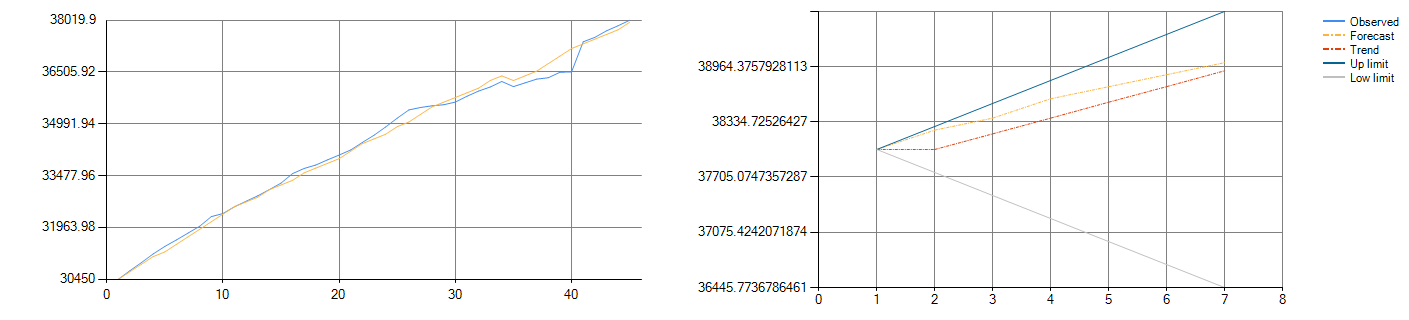図2-2：T 153量子適合（左）と予測（右）データ
図示するように、古典的なトレーニングによって生成される関数は線形であり、生成される確率予測は非線形である。図2−1は線形フィッティングと予測を示している：訓練と予測の結果はただの直線である。 図2−2は非線形フィッティングと予測を示している：フィッティングと予測結果の変動が大きい。
要するに、全体的な傾向だけを見たいのであれば、古典関数線形解析で十分であり、より詳細な近似推定を見たいのであれば、量子確率非線形解析でよい。
これは、すべてのタイプのデータセットに適したツールである新視Qの強力な機能と柔軟性を示しています。
3. 株式市場の予測
このケーススタディでは、新視Qは市場の最近の歴史を研究してトレンドを発見し、発見されたトレンドを利用して短期的に満足できる予測を行う。
図3-1は、トレーニング（左）と検証予測（右）の結果を示している。青線は観測データであり、黄色線は新視Q計算のデータであり、赤線は計算の全体的な傾向方向である。
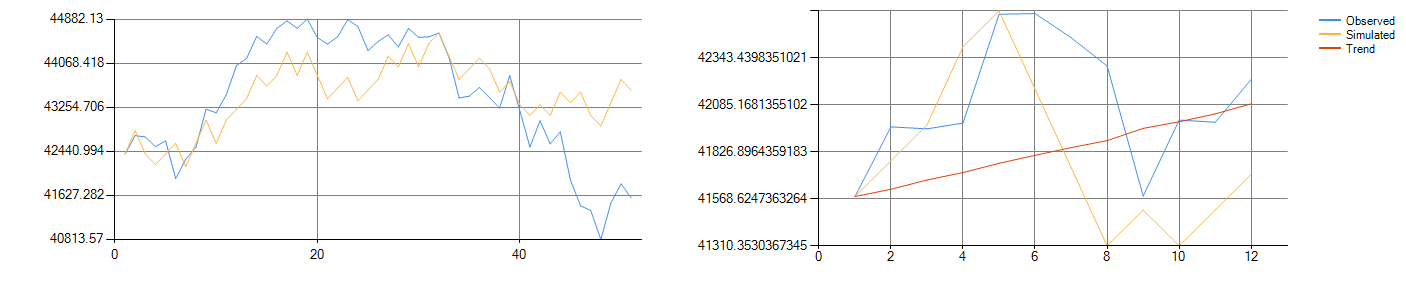図3-1：ダウ指数フィッティング（左）と検証予測（右）データ